自用的学习笔记,若有错误欢迎指出。
数据的表示【4】
进制的转换
按权展开法
R进制转十进制使用按权展开法,其具体操作方式为:将R进制数的每一位数值用$R^K$形式表示,即幂的底数是R,指数为k,k与该位和小数点之间的距离有关。当该位位于小数点左边,k值是该位和小数点之间数码的个数,而当该位位于小数点右边,k值是负值,其绝对值是该位和小数点之间数码的个数加1。
例如二进制:$10100.01 = 1 * 2^4 + 1 * 2^2 + 1 * 2^{-2}$
例如七进制:$604.01 = 6 * 7^2 + 4 * 7^0 + 1 * 7^{-2}$
二进制:0-1
十进制:0-9
十六进制:0-9,A-F(16进制数以大写’H’开头)
短除法
十进制转R进制使用短除法,也称为除基取余法。

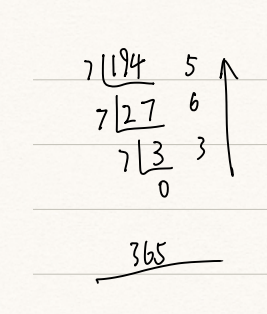
将二进制转为八进制和十六进制
#二进制转八进制
##将二进制数从右往左分成每3个数码一组
10 001 110
#转换
2 1 6
#二进制转十六进制
##将二进制数从右往左分成每4个数码一组
1000 1110
#转换
8 E注意:十六进制的1-15的表示方法

原码、反码、补码、移码
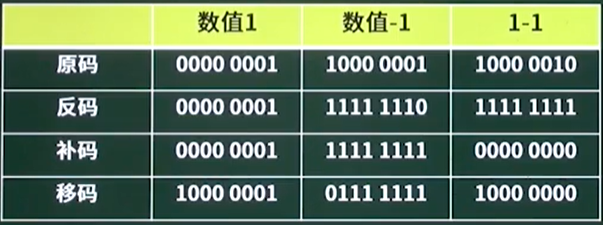
- 原码:符号位表示正负,
0表示+,1表示-。 - 反码:正数的反码和原码相同,负数按照各个数据位取反。
- 补码:正数的补码和原码相同,负数的补码按照其反码的基础上
+1。 - 移码:在补码的基础上在符号位(首位)上取反。
- 正数:原码、反码、补码相同,移码在符号位(首位)上取反。
- 负数:
- 反码:符号位不变,数据位取反。
- 补码:在反码的基础上
+1 - 移码:补码的基础上,符号位取反。
数值表示范围

当n = 8,也就是一共8个数位时:
- 定点整数:
- 虽然是通过
+1来实现了2^8,但是由于第一位是符号位,所以不显示,所以实际上1000 0000这个数无法显示出来。原码中正数和负数的数值表示范围为:$2^{n-1}$。同时,由于存在-0和+0这两个数(1000 0000&0000 0000),所以在正数和负数那里分别将那个-0或者+0去掉,所以需要$2^{n-1} - 1$。 - 原码表示范围:-127 ~ +127,转为二进制:
1111 1111~0111 1111。 - 补码表示范围:
1000 0000~0111 1111。其中,-128的补码为1 0000 0000是人为规定的。
- 虽然是通过
- 定点小数:
- 假设一个小数二进制表示:
0.111 1111在加上0.000 0001就可以得到1.000 0000。同理,定点小数中的负数和正数的表示范围为:$+(1 - 2^{n-1})$~$-(1 - 2^{n-1})$。 - 原码表示范围:
-0.111 1111~+0.111 1111。 - 补码表示范围:
-1~+0.111 1111。其中,-1的补码为1 0000 0000是人为规定的。
- 假设一个小数二进制表示:
注意:
- 原码和反码都存在
-0和+0这两个数。 - 在补码中的
-128和-1都是人为规定的。
浮点数运算
浮点数表示:$N = 尾数 * 基数^{指数}$
运算过程:对阶 > 尾数计算 > 结果格式化
特点:
- 一般尾数用补码,阶码用移码。
- 阶码的位数决定数的表示范围,位数越多范围越大。
- 尾数的位数决定数的有效精度,位数越多精度越高。
- 对阶时,小数向大数看齐。
- 对阶是通过较小的尾数右移实现的。
实例:
$1.25 * 10^5 + 2.25 * 10^7$ ,我们需要将$1.25 * 10^5$转换为——> $0.0125 * 10^7$,然后再进行运算为:$0.0125 * 10^5 + 2.25 * 10^7 = 2.2625 * 10^7$。
运算器与控制器【4】
计算机结构
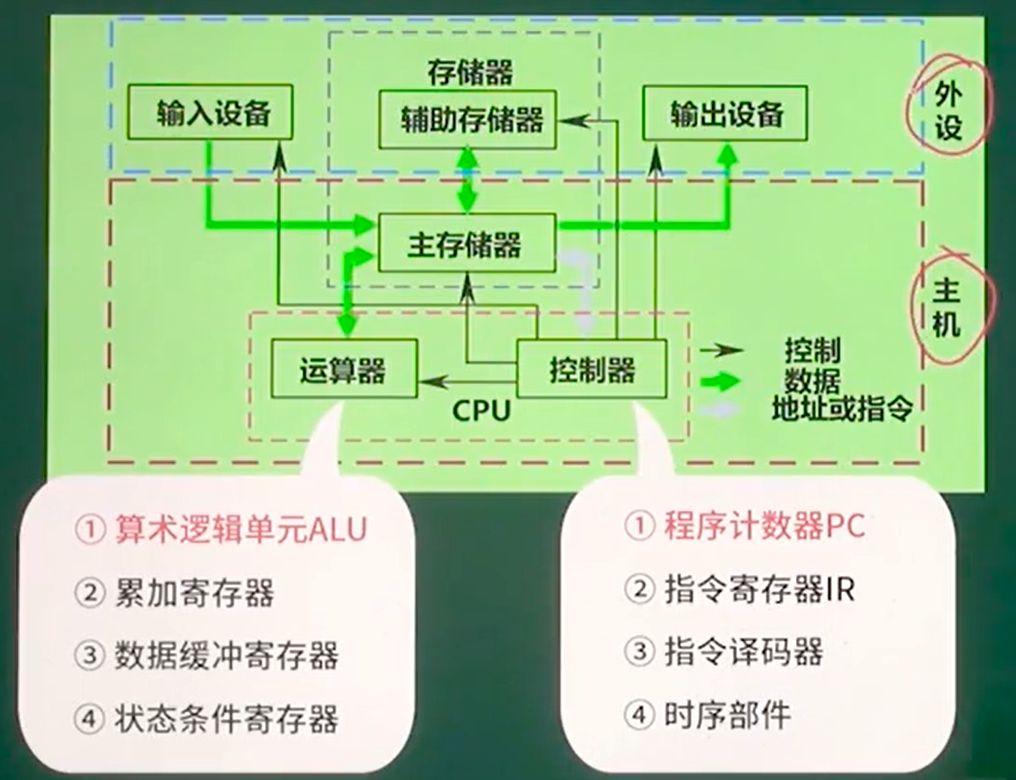
运算器:
- 算术逻辑单元ALU:数据的算数运算和逻辑运算。【重要】
- 累加寄存器AC:通用寄存器,为ALU提供一个工作区,用于暂存数据。【重要】
- 数据缓冲寄存器DR:写内存是,暂存指令或数据。
- 状态条件寄存器PSW:存状态标志与控制标志(争议:也有将其归为控制器)
控制器:
- 程序计数器PC:存储下一条要执行指令的地址。【重要】
- 指令寄存器IR:存储即将执行的指令。【重要】
- 指令译码器ID:对指令中的操作码字段进行分析解释。
- 时序部件:提供时序控制信号。
Flyuu分类法【2】
计算机体现结构分类-Flynn
I:指令流D:数据流S:单M:多
| 体系结构类型 | 结构 | 关键特性 | 代表 |
|---|---|---|---|
| 单指令流单数据流SISD | 控制部分:一个;处理器:一个;主存模块:一个 | 单处理器系统 | |
| 单指令流多数据流SIMD | 控制部分:一个;处理器:多个;主存模块:多个 | 各处理器以异步的形式执行同一条指令 | 并行处理机;阵列处理机;超级向量处理机 |
| 多指令流单数据流MISD | 控制部分:多个;处理器:一个;主存模块:多个 | 被证明不可能,至少是不实际的 | 目前没有,有文献称流水计算机为此类 |
| 多指令流多数据流MIMD | 控制部分:多个;处理器:多个;主存模块:多个 | 能够实现作业、任务、指令等各级全面并行 | 多处理系统;多计算机 |
CISC与RISC【2】
| 指令系统类型 | 指令 | 寻址方式 | 实现方式 | 其他 |
|---|---|---|---|---|
| CISC(复杂) | 数量多,是有频率差别大,可变长格式 | 支持多种 | 微程序控制技术(微码) | 研制周期长 |
| RISC(精简) | 数量少,使用频率接近,定长格式,大部分为单周期指令,操作寄存器,只有load/store操作内存 | 支持方式少 | 增加了通用寄存器;硬布线逻辑控制为主;适合采用流水线 | 优化编译,有效支持高级语言。 |
CISC与RISC比较,分那些维度?
- 指令数量、指令使用频率,寻址方式,寄存器,流水线支持,高级语言支持
- CISC:复杂,指令数量多,频率差别大,多寻址
- RISC:精简,指令数量少,操作寄存器,单周期,少寻址,多通用寄存器,流水线
指令的基本概念
每一条指令就是计算机语言的一个语句,它是一组有意义的二进制代码,指令的基本格式如下:
| 操作码字段 | 地址码字段 |
|---|
操作码部分指出了计算机要执行什么性质的操作,如加法、减法、取数、存数等。地址码字段需要包含各操作数的地址及操作结果的存放地址等,从其地址结构的角度可以分为三地址指令、二地址指令、一地址指令和零地址指令。
三地址指令
| OP | A1 | A2 | A3 |
|---|
二地址指令
| OP | A1 | A2 |
|---|
一地址指令
| OP | A1 |
|---|
零地址指令
| OP |
|---|
寻址方式
- 立即寻址方式
- 特点:操作数直接在指令中,速度快,灵活性差
- 直接寻址方式
- 特点:指令中存放的是操作数的地址
- 间接寻址方式
- 特点:指令中存放了一个地址,这个地址对应的内容是操作数的地址
- 寄存器寻址方式
- 特点:寄存器存放操作数
- 寄存器间接寻址方式
- 特点:寄存器内存放的是操作数的地址
流水线技术【4】
流水线 - 概念
相关参数计算:流水线执行时间计算、流水线吞吐率、流水线加速比、流水线效率
流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。各种部件同时处理是针对不同指令而言的,它们可同时为多条指令的不同部分进行工作,以提高各部件的利用率和指令的平均执行速度。
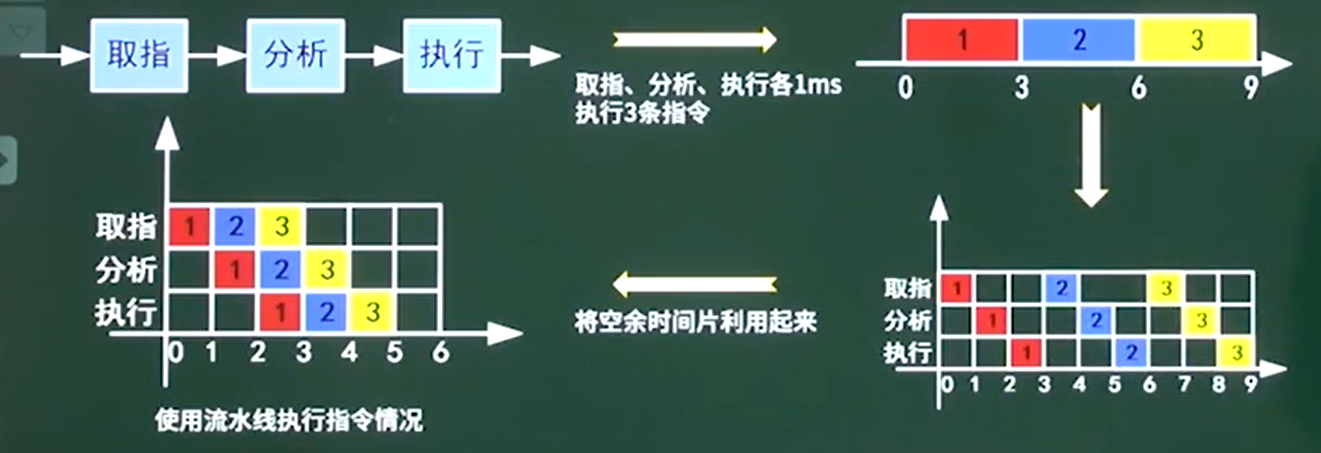
流水线 - 流水线计算
- 流水线建立时间:流水线第一条指令完成的时间
- 流水线周期:分段之后,指令当中执行时间最长的一段。
流水线计算公式为:
- 1条指令执行时间 + (指令条数 - 1)* 流水线周期
- 理论公式:(t1 + t2 + t3 +…+ tk) + (n - 1) * $\Delta t$
- 实践公式:k * $\Delta t$ + (n - 1) * $\Delta t$
(此处的$\Delta t$为流水线周期,而在题目中的$\Delta t$更多的指示的是单位时间)
例题:
- 一条指令的执行过程可以分解为取指、分析和执行三步,在取指时间t取指=3$\Delta t$、分析时间t分析=2$\Delta t$、执行时间t执行=4$\Delta t$的情况下,若按串行方式(顺序执行)执行,则10条指令全部执行完需多少个$\Delta t$?
- 由于是顺序执行,所以是求出一个指令建立的时间 * 全部指令个数
- (3 + 2 + 4) * $\Delta t$ * 10 = 90$\Delta t$
若按流水线的方式执行,流水线周期为多少个$\Delta t$?则10条指令全部执行完需要需多少个$\Delta t$?
- 流水线周期不用特地计算,直接判断在完成指令的过程中花费最长时间的是哪一段就好。
- 我们可以看出执行时间t执行=4$\Delta t$,在整个执行指令的过程中花费了最多的时间。所以,流水线周期就为:4$\Delta t$
- 则10条指令全部执行完需要需多少个$\Delta t$:((3 + 2 + 4) + (10 - 1) * 4) * $\Delta t$ = 45$\Delta t$
理论公式:(t1 + t2 + t3 +…+ tk) + (n - 1) * $\Delta t$
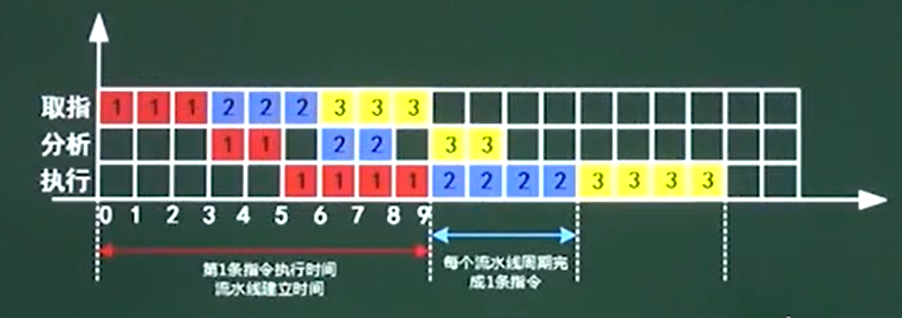
- 实践公式:k * $\Delta t$ + (n - 1) * $\Delta t$
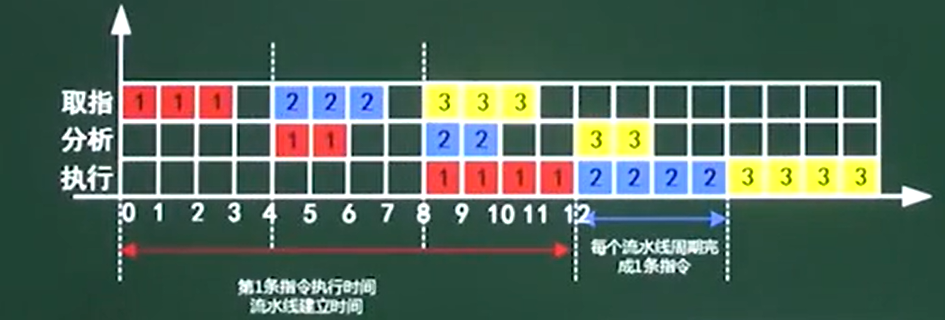
(注意:在选择题中,如果发现没有45$\Delta t$的选项出现的话,就需要套用实践公式来解题)
- 这里的指令执行周期还是4$\Delta t$
- 所以,套用公式:3 * 4$\Delta t$ + (10 - 1) * 4$\Delta t$ = 48$\Delta t$
流水线-流水线吞吐率计算
流水线的吞吐率(Though Put rate, TP)是指在单位时间内流水线所完成的任务数量或输出的结果数量。计算流水线吞吐率的最基本公式如下:TP = 指令条数 / 流水线执行时间
流水线最大吞吐率:流水线最大吞吐率 = 流水线周期的倒数
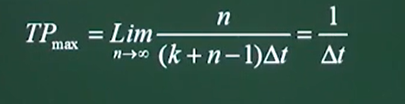
流水线-超标量流水线
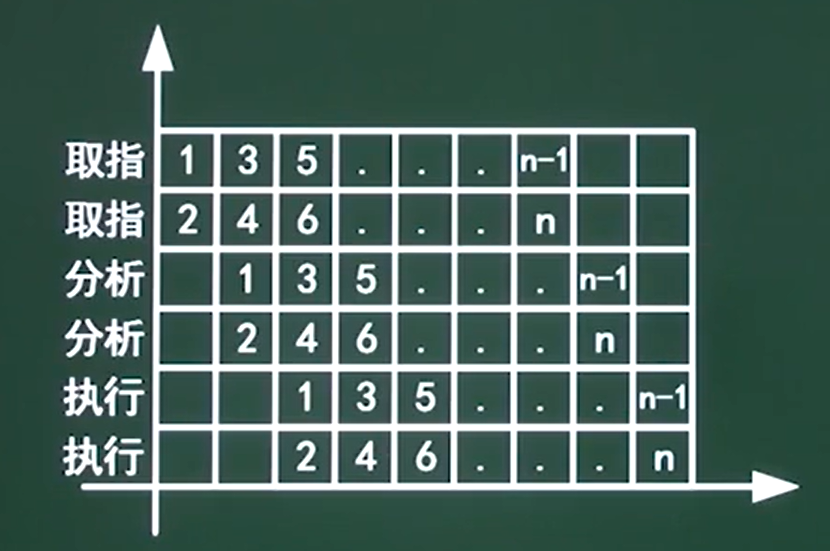
新提出一个参数:度。
度:指的是在某一时刻、某一个部件它可以同时处理的指令数量。



